호다닥 톺아보는 Vector

Overview

요새 어쩌다보니 데이터 엔지니어링에 관심을 가지게 되었습니다.

데이터를 다룸에 있어 빠지지 않는 개념중 하나인 Vector!
고등학교때 기하와 벡터를 배웠다면 이름만은 익숙한 그녀석… 과연 요놈은 뭐길래 수학도 아닌 컴퓨터.. 그것도 데이터에 등장하는 걸까요?

간단하게 알아보도록 하겠습니다!

물리학적 & 수학적 관점의 Vector

우리에게 가장 익숙한 개념입니다.

물체의 운동을 묘사하기 위해 물리학자들의 연구로 탄생하였고, 크기와 방향을 함께 가지는 물리량을 Vector 라고 표현하기 시작했습니다.

예를 들어 A가 왼쪽으로 3m/s의 속력으로 달리고 B가 오른쪽으로 3m/s 속력으로 달린다면, 둘의 물리량(속력)는 3m/s로 동일하기때문에 같은 운동으로 취급되었지만
방향이라는 인자를 함께 포함하고 연산하기 위해 Vector라는 개념이 도입되었습니다.

그래서 이런 Vector를 수학적으로 계산하려면 어떻게 표현하여야 할까요?

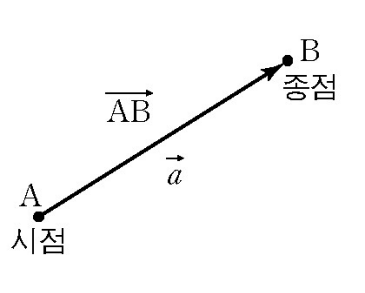
어떤 시점 A로부터 종점 B까지의 벡터를 \(\vec{AB}\) 이렇게 화살표를 사용하여 표현합니다.

위에서 예시로 든 물체의 속력을 벡터로 표현한다면, 화살표의 방향이 벡터의 방향이고, 화살표의 길이가 크기가 되겠습니다.

그러면 2차원 공간에서의 벡터를 생각해보겠습니다.

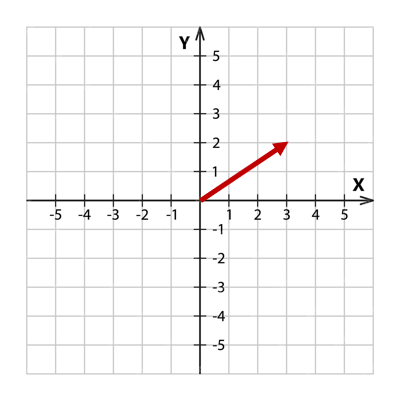
우리에게 익숙한 평면좌표계가 있고 x축(가로) y축(세로)을 기준으로 벡터를 표현할 수 있습니다.
그걸 점처럼 순서쌍으로 나타낼 수 있습니다. -> \((3,2)\)
혹은 2차원 행렬로도 나타낼 수 있습니다.

\[\left[\begin{array}{cc} 3\\ 2 \end{array}\right]\]

3차원은 어떨까요?

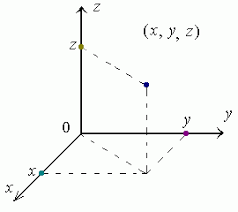
위와 같이 z축(높이)이 추가되었고 벡터는 가로,세로,높이를 모두 가진 순서쌍 혹은 3차원 행렬로 표현될 수 있을겁니다.

\[(x,y,z)\] \[\left[\begin{array}{cc} x\\ y \\z \end{array}\right]\]

4차원부터는 사실 3차원에 사는 우리들의 인지범위를 넘어서는 영역이기 때문에 그림으로 표현하기 어렵게 되지만,
벡터를 수식으로 표현할 수 있게된 우리들은 어렵지않게 그 형태를 예상할 수 있을 것입니다.
\((x,y,z,...)\)

\[\left[\begin{array}{cc} x\\ y \\z\\... \end{array}\right]\]

이것저것)
고등학교랑 대학때 배웠던 희미해진 기억만으로는 이 포스팅을 적기 힘들어서… 좀 찾아보니깐 엄밀히 따지면 위에서 언급한 Vector는 유클리드 기하학의 벡터(Euclidean Vector)만을 가리키는 좁은 정의라고 합니다.
비유클리드 기하학의 벡터로 넘어가면 또 정의가 달라진다는데 사실 아무리 읽어봐도 이해가 잘 안되어서 포기했읍니다…^^
대충 물리&수학 고수님들께서는 넓은 아량으로 봐주시면 감사하겠습니다.

DataScience에서의 Vector

그럼 이제 DataScience로 넘어와서 인터넷에 넘쳐나는 여러 데이터들을 생각해봅시다.
각종 원시데이터들은 분석 및 처리를 위해 의미있는 정보를 뽑아내 정형화하여 사용하게 됩니다.

정형화한다면 아래와 같은 형태로 될것입니다.

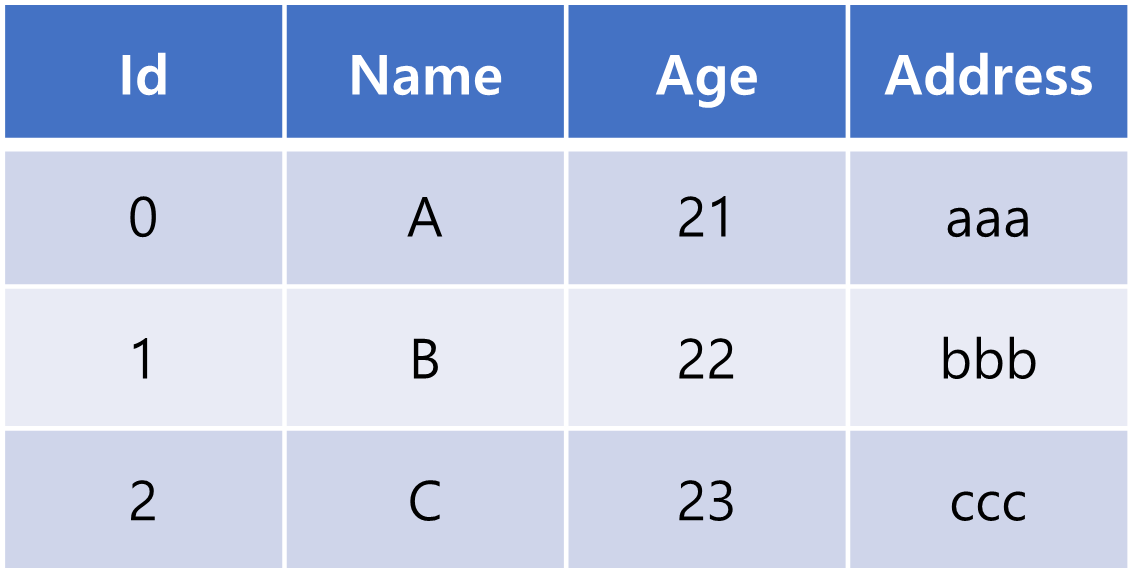
이 중 하나의 레코드를 뽑아서 수식의 형태로 표현한다면 아래와 같이 표현되겠죠!

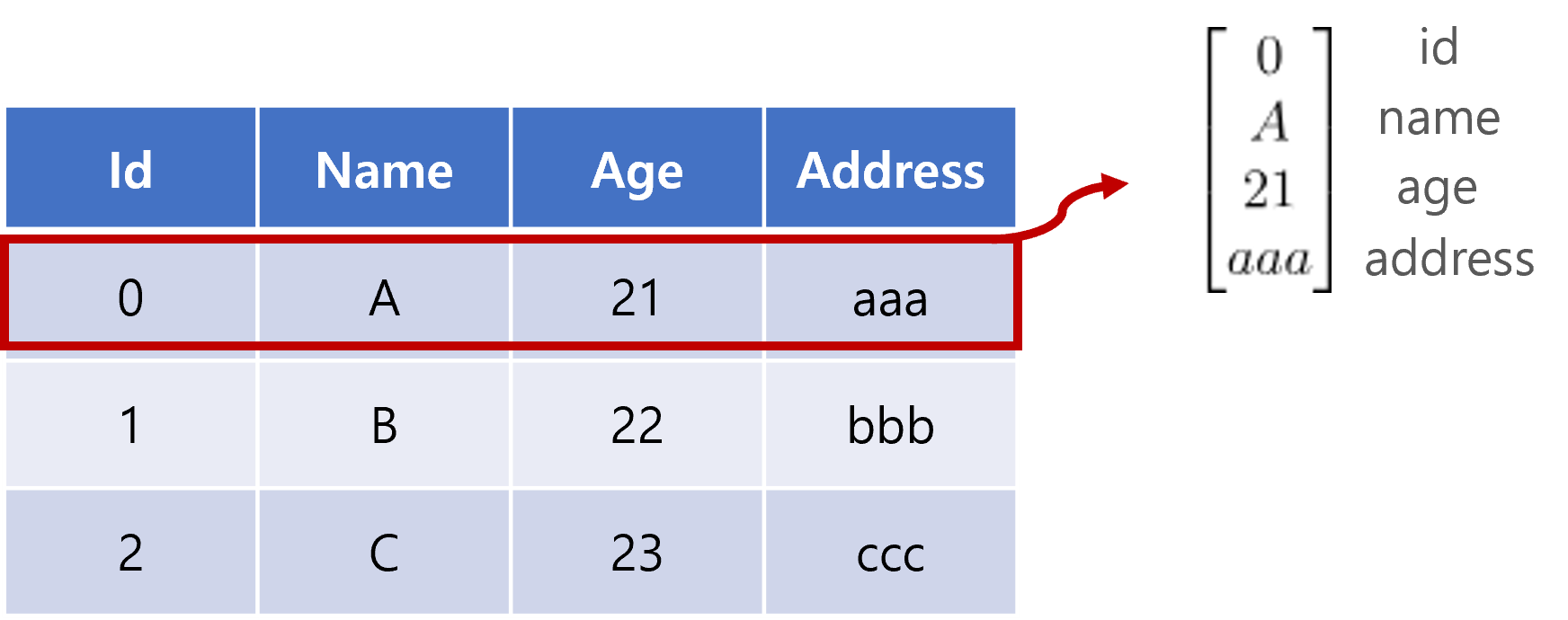
자세히 보니 위에서 봤던 수학의 벡터표현과 비슷합니다.
각 요소의 의미만 다르지 하나의 벡터안에 여러개의 인자가 들어가 있다는 점은 동일합니다.

위와 같이 데이터의 묶음은 여러의미의 데이터들로 이루어진 경우가 많은데, 이를 특정한 순서대로 모아둔 데이터 레코드를 선형대수에서는 Vector라고 부릅니다.
그리고 행렬(Matrix) 은 이러한 벡터가 여러개 있는 데이터의 집합이라고 생각하면 될 것 같습니다.

최초, 속력과 방향을 한번에 표현하기 위해 벡터라는 개념을 도입한 물리학과는 약간 의미가 달라지긴 했지만 더 넓은 의미의 개념이 된게 아닐까 개인적으로 생각하고 있습니다.

그래서 이렇게 데이터화된 벡터는 무작위로 뿌려진 데이터 뭉치들의 패턴들을 파악할 수 있게 도와주고, 연산에 대한 Global View를 보여줌으로써 데이터 분석을 할 수 있게 되는것이죠.

번외) STL(C++)에서의 Vector

사실 저는 vector라고 했을 때 가장 먼저 머리속에 떠올랐던 것은 수학과 물리에서 배웠던 벡터… 그리고 C++의 Vector입니다.

C++의 vector는 STL(Standard Template Library)에 포함된 클래스인데, Alexander Stepanov라는 디자이너에 의해 이름이 붙여졌습니다.

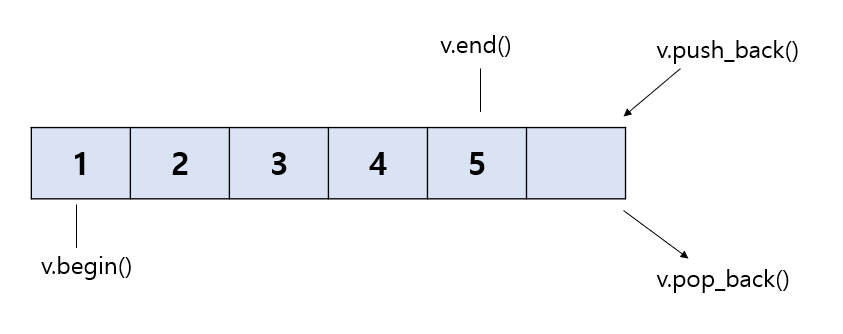
어떤 자료형도 넣을 수 있는 동적 배열이고, vector를 생성하면 메모리 heap에 생성되며 동적할당됩니다.
각 요소는 임의로 접근이 가능할 수 있고, 필요에 따라 유동적으로 크기를 조정할 수 있습니다.

그래서 이녀석이 수학적의미의 Vector랑 무슨관련이 있느냐..!

재밌게도 이 친구의 이름은 디자이너의 실수로 지어졌다고 합니다.

처음에는 기존 array와 다른 이름을 붙이고 싶어서 오래된 프로그래밍 언어인 Scheme과 Common Lisp에서 따와 vector라고 지었는데,
나중에 보니 더 오래된 수학적 의미의 vector와는 전혀 달랐던 겁니다(수학vector는 n개의 차원으로 배열을 구성할 수 있긴하지만 동적으로 크기가 늘어나지는 않음)

그러나 시간이 흘러 vector라는 이름을 고치기란 너무 어려워 그냥 내비뒀다고 한… 그런 비하인드 스토리가 있었다네요😅

디자이너의 저서 ->
“From Mathematics to Generic Programming” by Alexander Stepanov and Daniel Rose
The name vector in STL was taken from the earlier programming languages Scheme and Common Lisp. Unfortunately, this was inconsistent with the much older meaning of the term in mathematics and violates Rule 3; this data structure should have been called array. Sadly, if you make a mistake and violate these principles, the result might stay around for a long time.

관련 얘기가 나오는 유튜브 : spoils of the Egyptians: Lecture 2 Part2
(6분정도부터 나옴)

---